![]()
Cambia lo stile grafico in Bianco e Nero
Cambia lo stile grafico in Alto Contrasto
Cambia lo stile grafico in Solo Testo
Hai selezionato lo stile solo testo.
Home > Menu > Scheda del prodotto > Esperienza d'uso
Parole chiave: algoritmi, analisi numerica, calcolo algebrico, programmazione, metodo di eliminazione di Gauss, problema mal posto, polinomio interpolatore, funzione di Runge, formula di Lagrange
Maxima è un sistema di calcolo algebrico comprendente un linguaggio di programmazione semplice dal punto di vista della sintassi ma efficace, mediante il quale è possibile descrivere algoritmi per risolvere problemi da quelli classici (di ricerca, ordinamento, etc.) a quelli di analisi numerica. Grazie alla sintassi semplificata del linguaggio, le istruzioni possono essere apprese in tempi ridotti e manipolate senza particolari difficoltà: in questo modo l'attenzione rimane focalizzata sulla risoluzione del problema oggetto di analisi senza disperdersi negli aspetti di carattere formale, ed è possibile conseguire risultati significativi con ragionevole impegno.
La programmazione consente di perseguire importanti obiettivi formativi, fra i quali:
- favorire lo sviluppo di capacità metacognitive;
- acquisire la capacità di lavorare in gruppo attraverso la realizzazione di progetti complessi, e collaborare tra pari nella correzione degli errori dei programmi;
- stimolare negli studenti spirito critico e curiosità intellettuale, permettendo loro di costruire in modo autonomo funzionalità che i vari ambienti rendono disponibili già predefinite.
E' fondamentale, ai fini di promuovere un apprendimento significativo, che la programmazione non venga trascurata, invertendo la tendenza ad abbandonarla che molti docenti hanno assunto, essenzialmente a causa della sproporzione tra lo sforzo prodigato e l'esiguità dei risultati conseguiti.
Vengono di seguito presentate alcune esperienze di programmazione, realizzate nell'ambito del triennio ad indirizzo Brocca scientifico tecnologico presso il Liceo scientifico "G. Ricci Curbastro" di Lugo(RA), che utilizzano moduli sviluppati mediante tale linguaggio, nell'intento di proporre Maxima ai docenti di Matematica come strumento per fare programmazione nell'ambito della disciplina "Matematica e Informatica".
Grafica a raster-scan: algoritmo di Bresenham per la generazione di linee (classe quarta)
Zeri di una funzione (classe quinta)
Interpolazione statistica (classe quinta)
Alcuni esempi di sistemi la cui risoluzione costituisce un problema mal posto
Risolviamo il sistema:
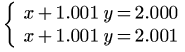
(C1)
solve([x+1.001*y=2.000,x+1.000*y=2.000],[x,y]);
(D1)
[[x=2,y=0]]
Perturbando lievemente il termine noto della prima equazione sulla terza cifra decimale e risolvendo il nuovo sistema, si ottiene una soluzione completamente diversa dalla precedente:
(C2)
solve([x+1.001*y=2.001,x+1.000*y=2.000],[x,y]);
(D2)
[[x=1,y=1]]
Questa lieve variazione del termine noto ha prodotto una rilevante modifica nella soluzione.
Il problema di risolvere un sistema tale che una piccola variazione dei coefficienti e/o dei termini noti determini una rilevente modifica della soluzione, si dice mal posto e la matrice dei coefficienti mal condizionata.
Se un problema è mal posto, l'errore inerente, dovuto alla rappresentazione dei dati iniziali del problema, prevale sull'errore algoritmico, cioè sugli errori di arrotondamento determinati dalle operazioni di calcolo eseguite: la bontà del risultato è pregiudicata a prescindere dal procedimento risolutivo utilizzato.
La sensibilità della soluzione del sistema rispetto a variazioni della matrice A dei coefficienti e del vettore b dei termini noti può essere misurata dall'indice di condizionamento di A, espresso in funzione della norma della matrice e della sua inversa:
cond(A)=||A|| ⋅||A - 1||
Se questo numero è piccolo allora il problema di risolvere il sistema Ax=b risulta ben posto e la matrice A ben condizionata, se è grande invece il problema può essere mal posto.
Classici esempi di matrici mal condizionate sono rappresentati dalla matrice di Vandermonde e dalla matrice di Hilbert.
Nel problema dell'interpolazione polinomiale, la matrice dei coefficienti è una matrice di Vandermonde. Vediamo un esempio con n=3, cioè supponendo di voler interpolare 4 punti: imponendo il passaggio del generico polinomio di grado 3 per i 4 punti, otteniamo un sistema di 4 equazioni nelle 4 incognite a0, a1, a2, a3 che rappresentano i coefficienti del polinomio.
(C1)
e0:a0+a1*x0+a2*(x0)^2+a3*(x0)^3=y0;
(D1) A3 x03 + A2
x02 + A1 x0 + a0=y0
(C2)
e1:a0+a1*x1+a2*(x1)^2+a3*(x1)^3=y1;
(D2)
A3 x13 + A2 x12
+ A1 x1 + a0=Y1
(C3)
e2:a0+a1*x2+a2*(x2)^2+a3*(x2)^3=y2;
(D3) A3 x23 + A2 x22 + A1 x2 + a0=Y2
(C4)
e3:a0+a1*x3+a2*(x3)^2+a3*(x3)^3=y3;
(D4) A3 x33 + A2 x32 + A1 x3 + a0=Y3
Determiniamo la matrice dei coefficienti, verificando che è effettivamente una matrice di Vandermonde:
(C5)
v4:coefmatrix([e0,e1,e2,e3],[a0,a1,a2,a3]);
(D5)
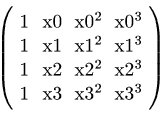
Valutiamo gli elementi della matrice attribuendo dei valori alle ascisse dei punti base:
(C6)
v4e:ev(v4,x0=1,x1=1.3,x2=2,x3=2.5);
(D1) v4
Determiniamo la matrice inversa:
(C2)
v4e_1:invert(v4e);
(D7)

Implementiamo l'algoritmo per il calcolo dell'indice di condizionamento della matrice di Vandermonde dell'esempio
(C8)
normainf(A,n):=block([somma,i,j,max], max:0, for i:1 step 1 thru n do (somma:abs(A[i,1]),for j:2 step 1 thru n do (somma:somma+abs(A[i,j])), if somma¿max then max:somma),return(max))$
Calcoliamo l'indice di condizionamento:
(C9)
condv4:normainf(v4e,4)*normainf(v4e_1,4);
(D9) 2245.888888888898
All'aumentare dell'ordine della matrice, l'indice di condizionamento cresce rapidamente a causa della crescita, in valore assoluto, degli elementi della matrice inversa.
Studio del polinomio interpolatore della funzione di Runge con utilizzo della formula di Lagrange
Esprimiamo il polinomio interpolatore mediante la formula di Lagrange:
pn(x)=∑ni=0yiLi(x)
I polinomi Li(x) soddisfano le condizioni
![]()
pertanto sono espressi dalla formula.
Studiamo ora come varia l'errore di interpolazione
R(x)=pn(x) - F(x)
per la funzione di Runge
![]()
al variare del numero dei punti base e quindi del grado del polinomio interpolatore, considerando ascisse equidistanti sull'intervallo [-1,1]
(C1)
f(x):=1/(1+25*x^2);
(C2)
h5:2/5;
(C3)
h7:2/7;
(C4)
h10:2/10;
(C5)
x5[0]:-1;
(C6)
y5[0]:1/26;
(C7)
for i:1 step 1 thru 5 do (x5[i]:x5[i-1]+h5, y5[i]:f(x5[i]));
(C8)
x7[0]:-1;
(C9)
y7[0]:1/26;
(C10)
for i:1 step 1 thru 7 do (x7[i]:x7[i-1]+h7, y7[i]:f(x7[i]));
(C11)
x10[0]:-1;
(C12)
y10[0]:1/26;
(C13)
for i:1 step 1 thru 10 do (x10[i]:x10[i-1]+h10, y10[i]:f(x10[i]));
(C14)
elle(j,n,x,vx):=block([p,i], p:1, for i:0 step 1 thru n do (if i#j then p:p*((x-vx[i])/(vx[j]-vx[i])) ),return(p))$
(C15)
l(n,x,vx,vy):=block([p,i], p:0, for i:0 step 1 thru n do ( p:p+ vy[i]* elle(i,n,x,vx) ),return(p))$
(C16)
plot2d([l(5,x,x5,y5),l(7,x,x7,y7),l(10,x,x10,y10),f(x)],[x,-1,1],[y,-1,10]);
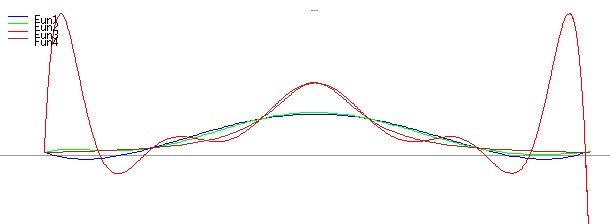
Dal grafico si osserva che, aumentando il numero dei punti base con ascisse equidistanti e quindi il grado del polinomio interpolatore, l'errore di interpolazione diminuisce nella parte centrale dell'intervallo ma aumenta in modo vistoso in prossimità degli estremi dell'intervallo steesso.
Studio del polinomio interpolatore della funzione di Runge con utilizzo della formula di Newton delle differenze divise
Esprimiamo il polinomio interpolatore mediante la formula di Newton delle differenze divise:
pn(x)=F(x0) + (x - x 0)F[x0,x1] + (x - x 0)(x - x 1)F[x0,x1,x2] + … + (x - x 0)…(x - x n - 1)F[x0,…,xn]
essendo le differenze divise definite dalle formule ricorrenti:
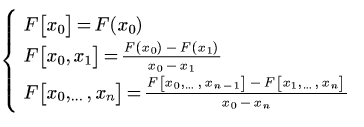
(C1)
f(x):=1/(1+25*x^2);
(C2)
h5:2/5;
(C3)
x5[0]:-1;
(C4)
y5[0]:1/26;
(C5)
dd5[0]:y5[0];
(C6)
h10:2/10;
(C7)
x10[0]:-1;
(C8)
y10[0]:1/26;
(C9)
dd10[0]:y10[0];
(C10)
for i:1 step 1 thru 5 do (x5[i]:x5[i-1]+h5, y5[i]:f(x5[i]), dd5[i]:y5[i]);
(C11)
for i:1 step 1 thru 10 do (x10[i]:x10[i-1]+h10, y10[i]:f(x10[i]), dd10[i]:y10[i]);
(C12)
diffdivi(n,vx):=block([k,i], for i:1 step 1 thru n do (for k:n step -1 thru i do (if vx=x10 then dd10[k]:(dd10[k]-dd10[k-1])/(vx[k]-vx[k-i]) else dd5[k]:(dd5[k]-dd5[k-1])/(vx[k]-vx[k-i]) ) ))$
(C13)
diffdivi(5,x5);
(C14)
diffdivi(10,x10);
(C15)
newton(n,x,vx,dd):=block([p,i], p:dd[n], for i:n-1 step -1 thru 0 do (p:p*(x-vx[i])+dd[i]), return(p))$
(C16)
plot2d([newton(5,x,x5,dd5),newton(10,x,x10,dd10),f(x)],[x,-1,1],[y,-1,10]);
Mettiamo ora a confronto il polinomio di interpolazione di grado n=10 con ascisse
xi= - 1 + i h i=1,2,…,n equidistanti di passo h=2/n , con il polinomio di interpolazione di grado
n=10 avente come ascisse gli n + 1 zeri del polinomio di Chebyshev di grado n + 1=11
xi=cos(frac ((2(n - i) + 1)π, 2(n + 1))) i=0,1,…,n .
Ricordiamo che i polinomi di Chebyshev sull'intervallo [ - 1,1] sono definiti dalla formula ricorsiva
T0(x)=1 , T1(x)=x
Tk + 1(x)=2 x Tk(x) - Tk - 1(x) k=1,2,….,n - 1
(C1)
f(x):=1/(1+25*x^2);
(C2)
n:10;
(C3)
h10:2/n;
(C4)
xc10[0]:-1;
(C5)
yc10[0]:1/26;
(C6)
ddc10[0]:yc10[0];
(C7)
xe10[0]:-1;
(C8)
ye10[0]:1/26;
(C9)
dde10[0]:ye10[0];
(C10)
for i:1 step 1 thru n do (xe10[i]:xe10[i-1]+h10, ye10[i]:f(xe10[i]), dde10[i]:ye10[i], xc10[i]:cos(((2*(n-i)+1)*%pi)/(2*(n+1))), yc10[i]:f(xc10[i]), ddc10[i]:yc10[i] );
(C11)
diffdivi(n,vx):=block([k,i], for i:1 step 1 thru n do (for k:n step -1 thru i do (if vx=xe10 then dde10[k]:(dde10[k]-dde10[k-1])/(vx[k]-vx[k-i]) else ddc10[k]:(ddc10[k]-ddc10[k-1])/(vx[k]-vx[k-i]))))$
(C12)
diffdivi(n,xe10);
(C13)
diffdivi(n,xc10);
(C14)
newton(n,x,vx,dd):=block([p,i], p:dd[n], for i:n-1 step -1 thru 0 do (p:p*(x-vx[i])+dd[i]),return(p))$
(C15)
plot2d([newton(10,x,xe10,dde10),newton(10,x,xc10,ddc10),f(x)],[x,-1,1],[y,-1,10]);
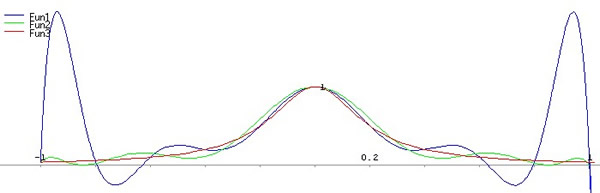
Dal grafico si può concludere che l'errore di interpolazione risulta minore se i punti base hanno come ascisse gli zeri del polinomio di Chebyshev.
Bibliografia
1) G.Casadei, M.Lacchini, Il Problem Solving algoritmico, Atti didamatica 2004, Omniacom, Ferrara, 2004
2) D.Bini, M.Capovani, O.Menchi, Metodi numerici per l'algebra lineare , Zanichelli, Bologna, 1988
3) S. Harrington, Computer Graphics, McGraw Hill, 1983
4) F.Fontanella, A.Pasquali, Calcolo numerico , Pitagora, Bologna, 1984
5) I.Galligani, Elementi di analisi numerica, Zanichelli, Bologna, 1987
6) A.Paoluzzi, Informatica grafica, La Nuova Italia Scientifica, 1988
7) D.F. Rogers, Procedural Elements for Computer Graphics, McGraw Hill, USA, 1985, ed.italiana Tecniche Nuove, Milano, 1988
8) J. Stoer, Einfuhrung in die Numerische Mathematik, Springer Verlag, Berlin-Heidelberg-New York,1972, ed. italiana Zanichelli, Bologna, 1974
Vai alla pagina 1 2