![]()
Interpolazione matematica (classe quinta)
Cambia lo stile grafico in Bianco e Nero
Cambia lo stile grafico in Alto Contrasto
Cambia lo stile grafico in Solo Testo
Hai selezionato lo stile solo testo.
Home > Menu > Scheda del prodotto > Esperienza d'uso
Parole chiave: algoritmi, analisi numerica, calcolo algebrico, programmazione, metodo di eliminazione di Gauss, problema mal posto, polinomio interpolatore, funzione di Runge, formula di Lagrange
Maxima è un sistema di calcolo algebrico comprendente un linguaggio di programmazione semplice dal punto di vista della sintassi ma efficace, mediante il quale è possibile descrivere algoritmi per risolvere problemi da quelli classici (di ricerca, ordinamento, etc.) a quelli di analisi numerica. Grazie alla sintassi semplificata del linguaggio, le istruzioni possono essere apprese in tempi ridotti e manipolate senza particolari difficoltà: in questo modo l'attenzione rimane focalizzata sulla risoluzione del problema oggetto di analisi senza disperdersi negli aspetti di carattere formale, ed è possibile conseguire risultati significativi con ragionevole impegno.
La programmazione consente di perseguire importanti obiettivi formativi, fra i quali:
- favorire lo sviluppo di capacità metacognitive;
- acquisire la capacità di lavorare in gruppo attraverso la realizzazione di progetti complessi, e collaborare tra pari nella correzione degli errori dei programmi;
- stimolare negli studenti spirito critico e curiosità intellettuale, permettendo loro di costruire in modo autonomo funzionalità che i vari ambienti rendono disponibili già predefinite.
E' fondamentale, ai fini di promuovere un apprendimento significativo, che la programmazione non venga trascurata, invertendo la tendenza ad abbandonarla che molti docenti hanno assunto, essenzialmente a causa della sproporzione tra lo sforzo prodigato e l'esiguità dei risultati conseguiti.
Vengono di seguito presentate alcune esperienze di programmazione, realizzate nell'ambito del triennio ad indirizzo Brocca scientifico tecnologico presso il Liceo scientifico "G. Ricci Curbastro" di Lugo(RA), che utilizzano moduli sviluppati mediante tale linguaggio, nell'intento di proporre Maxima ai docenti di Matematica come strumento per fare programmazione nell'ambito della disciplina "Matematica e Informatica".
Grafica a raster-scan: algoritmo di Bresenham per la generazione di linee (classe quarta)
Zeri di una funzione (classe quinta)
![]()
Interpolazione matematica (classe quinta)
Interpolazione statistica (classe quinta)
Dati n + 1 punti (xi,yi) con ascisse tutte distinte, il problema dell'interpolazione matematica può presentarsi nelle seguenti situazioni:
Interpolare gli n + 1 punti significa determinare una funzione y=f(x) passante per i punti assegnati, cioè tale che f(xi)=yi i=0,1,…,n
Si può assumere in molti casi che la funzione y=f(x) abbia l'espressione
y=a0 ɸ 0(x) + a1 ɸ 1(x) + …. + an ɸ n(x)
dove ϕi(x) sono funzioni elementari quali ad esempio i monomi 1, x, ..., xn : in tal caso la funzione interpolatrice sarà un polinomio di grado al piu' n
pn(x)=a0 + a1x + …. + anxn
che può essere valutato, differenziato o integrato facilmente in un numero finito di intervalli, usando solo le operazioni aritmetiche fondamentali di addizione, sottrazione e moltiplicazione.
Nell'ipotesi in cui gli n+1 punti abbiano ascisse tutte distinte, esiste un solo polinomio che li interpola; tale polinomio può essere determinato:
- risolvendo il sistema lineare normale pn(xi)=yi i=0,1,…,n nelle n+1 incognite a0, a1, …,an, ad esempio mediante il metodo di Gauss. La matrice dei coefficienti è una matrice di Vandermonde: essendo le ascisse xi tutte distinte, è non singolare quindi il sistema ammette una sola soluzione, tuttavia questa matrice risulta mal condizionata, quindi il problema di risolvere tale sistema è in generale mal posto;
- mediante la formula di Lagrange;
- mediante la formula di Newton, nelle situazioni 2 e 3.
Aumentando il numero dei punti base, aumenta anche il grado del polinomio, ma in generale non diminuisce l'errore di interpolazione, come si può dedurre dagli esempi di seguito proposti.
Risoluzione di un sistema lineare normale con matrice dei coefficienti non singolare applicando il metodo di eliminazione di Gauss
Ricordiamo che un sistema di equazioni si definisce lineare se costituito di equazioni lineari, cioè le incognite che compaiono in esse hanno grado al piu' uguale a 1, normale se il numero delle equazioni è uguale al numero delle incognite, compatibile o consistente se ammette almeno una soluzione.
Sia
assegnato il sistema lineare normale di ordine n
Ax=b dove A=[a] è la matrice dei coefficienti,
b=(b1,…,bn)
il vettore dei termini noti e x=(x1,…,xn)
il vettore soluzione. Se la matrice A
dei coefficienti è non singolare (cioè
ammette matrice inversa A - 1), il
metodo di eliminazione di Gauss consente di risolvere
il sistema con un costo computazionale dell'ordine di
![]() .
Applicando alla matrice A
e al vettore b
le trasformazioni elementari di Gauss, il sistema viene
trasformato in un sistema triangolare superiore equivalente
che può essere risolto mediante sostituzione
all'indietro.
.
Applicando alla matrice A
e al vettore b
le trasformazioni elementari di Gauss, il sistema viene
trasformato in un sistema triangolare superiore equivalente
che può essere risolto mediante sostituzione
all'indietro.
Consideriamo il sistema
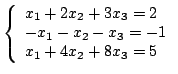
Poniamo
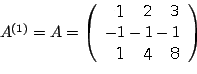
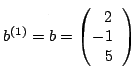
Determiniamo ora nella prima colonna un elemento a(1)r1≠0, quindi scambiamo la riga 1 con la riga r sia nella matrice A(1) sia nel vettore b(1) (nell'esempio risulta a(1)11≠0 pertanto non effettuiamo alcuno scambio); se non esiste alcun indice r tale che a(1)r1≠0, la matrice A(1) è singolare e il metodo si arresta.
Si definiscono elemento pivot l'elemento a(1)11 risultante e pivoting per colonna il procedimento di ricerca applicato.
Consideriamo la trasformazione elementare di Gauss di indice 1:
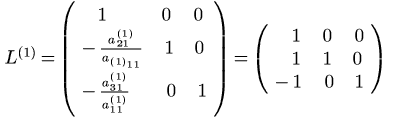
Applichiamo L(1) alla matrice dei coefficienti e al vettore dei termini noti (mediante prodotto righe per colonne) ottenendo i corrispondenti trasformati:
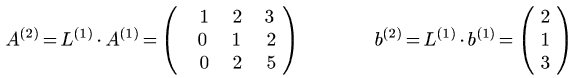
La trasformazione L(1) elimina x1
dalla seconda e dalla terza equazione: alla seconda
equazione sostituisce la somma della seconda equazione
con la prima moltiplicata per![]() ,
alla terza equazione sostituisce la somma della terza
equazione con la prima moltiplicata per
,
alla terza equazione sostituisce la somma della terza
equazione con la prima moltiplicata per ![]() .
.
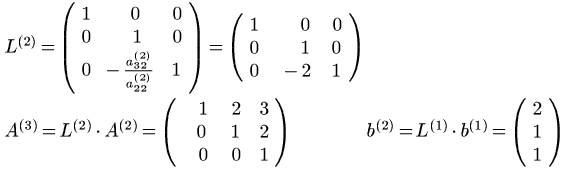
La trasformazione L(2), applicata
alla matrice A(2), elimina x2
dalla terza equazione, sostituendo ad essa la somma
della terza equazione con la seconda moltiplicata per
![]()
Il sistema dato risulta così trasformato nel sistema triangolare superiore equivalente:
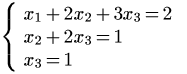
che si risolve mediante sostituzione all'indietro a partire dall'ultima equazione:
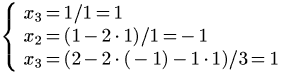
Osserviamo che:
L(2)⋅L(1)⋅A=A(2)
da cui discende la seguente fattorizzazione della matrice A:
A=(L(2)⋅L(1)) - 1⋅A(2)=(L(1)) - 1⋅(L(2)) - 1⋅A(2)= L⋅R
doveL=(L(1)) - 1⋅(L(2)) - 1è una matrice triangolare inferiore con elementi sulla diagonale principale tutti uguali a 1, e R=A(2) è una matrice triangolare superiore con elementi sulla diagonale principale tutti diversi da 0.
Per un sistema lineare normale di ordine n, al passo k 1≤ k ≤ n - 1 si applica la trasformazione elementare di Gauss
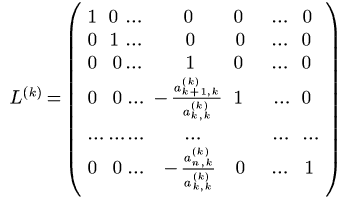
La matrice L(k) è triangolare inferiore con elementi sulla diagonale principale tutti diversi da 0, quindi è non singolare cioè ammette matrice inversa

Per ridurre gli errori di troncamento, in generale si sceglie come elemento pivot il massimo, in valore assoluto, fra gli elementi della colonna presi in esame ossia
![]()
questo criterio di scelta tuttavia garantisce la stabilità numerica del metodo di Gauss solo in particolari condizioni [7].
Applichiamo ora il metodo al sistema iniziale utilizzando Maxima. Per comodità consideriamo la matrice completa del sistema, ottenuta giustapponendo alla matrice dei coefficienti il vettore dei termini noti:
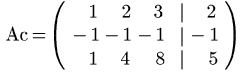
Il caricamento della matrice può avvenire:
- a partire dalle equazioni del sistema mediante la funzione AUGCOEFMATRIX, che restituisce la matrice completa del sistema, coi termini noti trasportati al primo membro e quindi nell'ultima colonna con segno cambiato:
- mediante il comando ENTERMATRIX che chiede in input i singoli elementi.
Definiamo la lista con le equazioni del sistema:
(C1)
[x1+2*x2+3*x3=2,-x1-x2-x3=-1,x1+4*x2+8*x3=5];
(D1)
[3 x3 + 2 x2 + x1=2, - x3 - x2 - x1= - 1,8 x3 + 4 x2 + x1=5]
Generiamo la matrice completa del sistema:
(C2)
Ac:augcoefmatrix(%,[x1,x2,x3]);
(D2)
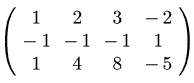
Mediante la funzione TRIANGULARIZE applichiamo le trasformazioni elementari di Gauss alla matrice dei coefficienti e al vettore dei termini noti, ottenendo la matrice A(2) e il vettore - b(2) già descritti in precedenza:
(C3)
Ac2:triangularize(Ac);
(D3)
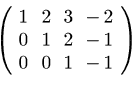
Implementiamo il sottoprogramma che risolve il sistema triangolare superiore:
(C4)
risolvits(A,n):=block([i,j,somma],if A[n,n]=0 then (print("coefficiente di x",n,"=0"),return("matrice dei coefficienti singolare")) else(x[n]:-A[n,n+1]/A[n,n], for i:(n-1) step -1 thru 1 do (somma:0, for j:(i+1) step 1 thru n do (somma:somma+A[i,j]*x[j]),x[i]:(-A[i,n+1] somma)/A[i,i]),stampasol(x,n),return("stampa soluzione effettuata")))$
(C5)
stampasol(x,n):=block([i], for i:1 step 1 thru n do (print("x",i,"=",x[i])))$
(C6)
risolvits(Ac2,3);
x1=1
x2= - 1
x3=1
(D7) stampa soluzione effettuata
(C8)
[x1+x2+2*x3=2,2*x1-x2+x3=1,x1+2*x2+3*x3=2];
(D8)
[2 x3 + x2 + x1=2,x3 - x2 + 2 x1=1,3 x3 + 2 x2 + x1=2]
(C9)
Ac:augcoefmatrix(%,[x1,x2,x3]);
(D9)
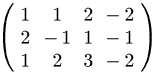
(C10)
Ac2:triangularize(Ac);
(D10)
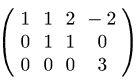
Si osservi che Maxima sceglie il pivot a(2)r2 nella terza riga, cioè privilegia la riga contenente il maggior numero di elementi nulli per ridurre le moltiplicazioni.
In questo esempio la matrice dei coefficienti è singolare e il sistema non compatibile
(C11)
risolvits(Ac2,3);
coefficiente di x3=0
(D11) matrice dei coefficienti singolare
(C12)
[x1+x2+x3=0,2*x1+x2-x3=-3,2*x1-4*x3=-6];
(D12)
[x3 + x2 + x1=0, - x3 + x2 + 2 x1= - 3,2 x1 - 4 x3= - 6] ;
(C13)
Ac:augcoefmatrix(%,[x1,x2,x3]);
(D13)
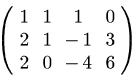
(C14)
Ac2:triangularize(Ac);
(D14)
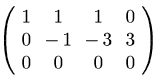
In questo caso la matrice R è singolare, come l'algoritmo segnala, ma il sistema è compatibile
(C15)
risolvits(Ac2,3);
coefficiente di x3=0
(D15) matrice dei coefficienti singolare
Verifichiamo ora le proprietà delle trasformazioni L(1) ed L(2), in quanto matrici triangolari inferiori.
(C1)
L1:entermatrix(3,3);
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
4
Row 1 Column 1:
1
Row 1 Column 2:
0
Row 1 Column 3:
0
Row 2 Column 1:
1
Row 2 Column 2:
1
Row 2 Column 3:
0
Row 3 Column 1:
-1
Row 3 Column 2:
0
Row 3 Column 3:
1
Matrix
entered.
(D1)
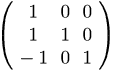
Verifichiamo ora che
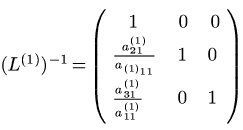
(C2)
L1_1:invert(L1);
(D2)
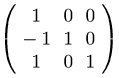
(C3)
L2:entermatrix(3,3);
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
4
Row 1 Column 1:
1
Row 1 Column 2:
0
Row 1 Column 3:
0
Row 2 Column 1:
0
Row 2 Column 2:
1
Row 2 Column 3:
0
Row 3 Column 1:
0
Row 3 Column 2:
-2
Row 3 Column 3:
1
Matrix entered.
(D3)
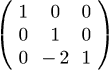
(C4)
L2_1:invert(L2);
(D4)
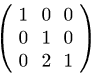
Verifichiamo infine che (L(2)⋅L(1)) - 1=(L(1)) - 1⋅(L(2)) - 1=L , essendo L ancora una matrice triangolare inferiore con elementi sulla diagonale principale tutti uguali a 1:
(C5)
prodl1l2:L1 . L2;
(D5)
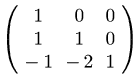
(C6)
prodl1l2_1:invert(prodl1l2);
(D6)
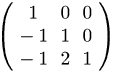
(C7)
L2_1 . L1_1;
(D7)
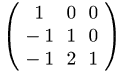
Bibliografia
1) G.Casadei, M.Lacchini, Il Problem Solving algoritmico, Atti didamatica 2004, Omniacom, Ferrara, 2004
2) D.Bini, M.Capovani, O.Menchi, Metodi numerici per l'algebra lineare , Zanichelli, Bologna, 1988
3) S. Harrington, Computer Graphics, McGraw Hill, 1983
4) F.Fontanella, A.Pasquali, Calcolo numerico , Pitagora, Bologna, 1984
5) I.Galligani, Elementi di analisi numerica, Zanichelli, Bologna, 1987
6) A.Paoluzzi, Informatica grafica, La Nuova Italia Scientifica, 1988
7) D.F. Rogers, Procedural Elements for Computer Graphics, McGraw Hill, USA, 1985, ed.italiana Tecniche Nuove, Milano, 1988
8) J. Stoer, Einfuhrung in die Numerische Mathematik, Springer Verlag, Berlin-Heidelberg-New York,1972, ed. italiana Zanichelli, Bologna, 1974
Vai alla pagina 1 2